Математичко клатно
Математичко клатно је тело занемарљивих димензија али не и занемарљиве масе, обешено о неистегљиву нит занемарљиве масе.
Период осциловања математичког клатна :
Ово је математички модел који у природи највише подсећа на металну куглицу обешену о неистеглјиву нит. Неопходно је да је димензија мала да би смањили утицај отпора средине и тиме избегли да се добије пригушено осциловање. Значајно је и да има масу јер се креће под дејством гравитационе силе. Када би конопац био истегљив ( рецимо као клоптица са гумом) осцилације би биле непрвилне.
Период осциловања математичког клатна је:
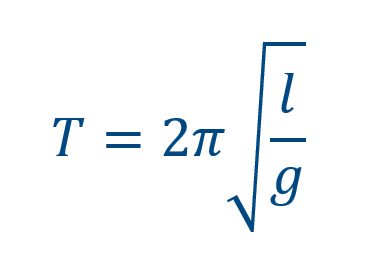
Његов мериод осциловања зависи од l-дужине нити и g-гравитационог убрзања планете.
Закон одржања енергије код осцилатора.
Закон одржања енергије: Енергија се не може ни створити ни уништити већ се само може претворити из једног облика у други. У изолованом систему укупна енергија је увек иста. Можете се подсетити лекције о енергији.
Код осцилаторног кретања кинетичка енергија се претвара у потенцијалну и потенцијална у кинетичку.
У амплитудном положају мирује па је Ек=0, Ер=највећа јер је висина највећа; у равнотежном положају је обрнто, брзина је максимална па је и кинетичка максимална Ек=највеће, Ер=0, а висина је једнака нули па је и потенцијална једнака нули. При преласку из амплитудног у равнотежни потенцијална се претвори у кинетичку, а из равнотежног у амплитудни кинетичка у потенцијалну.
ЗАДАТАК:
- Колика је кинетичка енергија у амплитудном и равнотежном положају ако је потенцијална енергија у амплитудном положају 10Ј?
- Израчунај брзину осцилатора у равнотежном положају ако је маса куглице 10 g, а укупна енергија је 2Ј.
- Pogledaj simulaciju:
https://phet.colorado.edu/sims/html/pendulum-lab/latest/pendulum-lab_all.html?locale=sr

